Q-learning의 직관적 이해
이번 시간에는 Q learning에 대해 배울 것이다.
여기 Bellman Equation 이 있다.
$$ V(s) = \underset{a}{max} [R(s,a)+\gamma \sum_{s^\prime}P(s,a,s^\prime)V(s^\prime))] $$
근데 여기서 Q는 어디에 있는 걸까?
왜 Q learning이라고 하는 걸까?
여기 좋은 예시가 있다
Agent의 그림을 귀엽게 바꿔봤다
reward = -1 도 해골이 아닌 불로 표현해봤다.

여튼 여기서 Markov decision process이기 때문에,
agent가 어떻게 왔는지에 대해서는 중요하지 않다.
그래서 어디로 갈지 최적의 결정을 내릴 때, 과거는 고려하지 않고
현재와 미래의 상태만을 고려했다.
또한 표를 보면 3가지 갈 수 있는 경우의 수가 존재하는데,
경험에 따라 각 state의 value를 계산했고 이를 V(s)로 표현했다.
살짝 수정을 해보겠다
똑같은 개념과 똑같은 문제를 가지고 할껀데,
대신 각 상태의 가치를 보는 것이 아니라 각 행동의 가치를 볼 예정이다.
이때 상태가치가 아니므로 더이상 $ V(s) $ 로 쓰지 않고, $ Q(현재상태, action) $으로 쓰도록 하겠다.
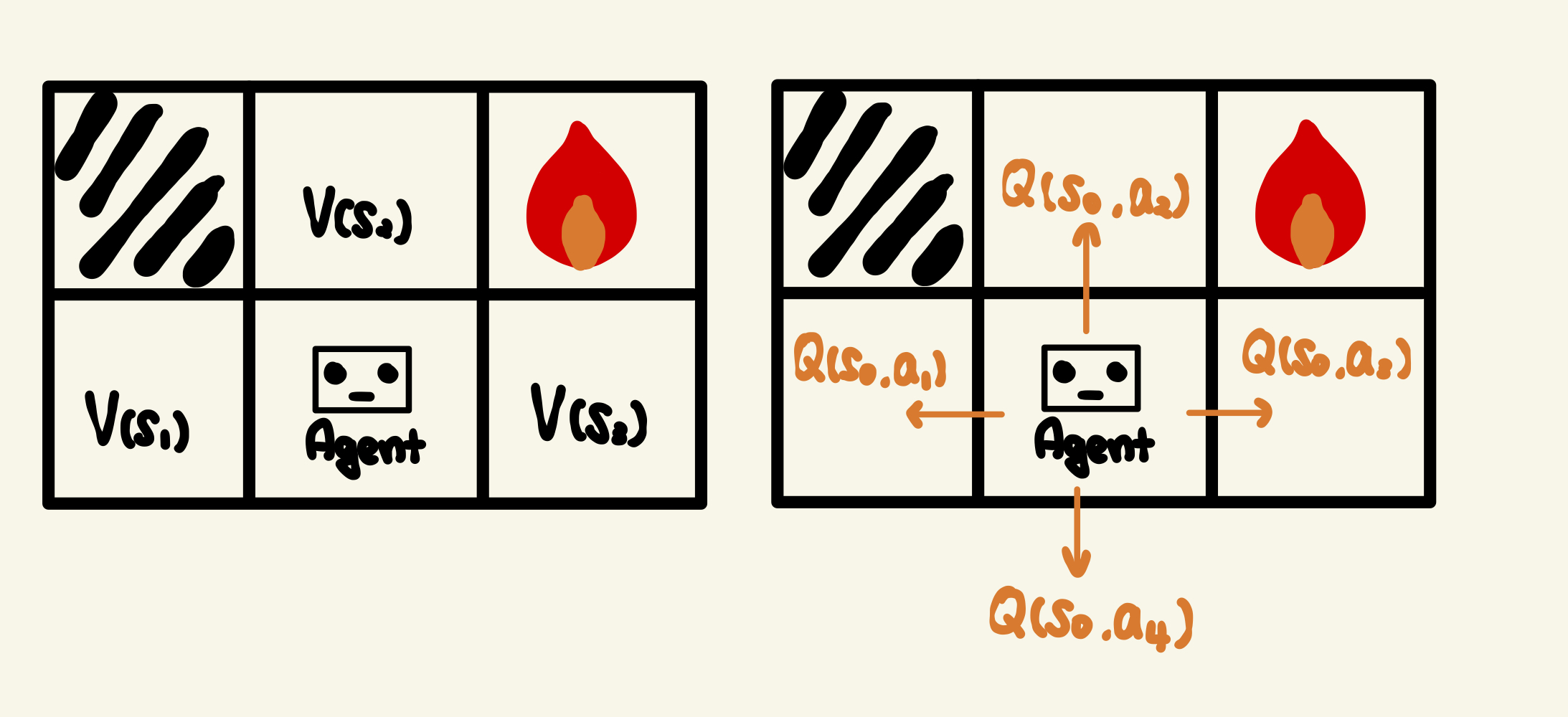
여기서 왜 하필 Q를 쓰냐에 많은 답들이 존재하는데 나도 잘 모르겠다.
대신에 "Quality of action" 이라는 말이 제일 끌려서 행동의 퀄리티라고 생각하도록 하겠다.
여기서 Q를 어떻게 정량화할까?
Let's formula Q !
위의 두 사진에서 V(s)나 Q(s,a)나 분명 연관성이 있을 수 밖에 없다는 것은 다들 눈치를 챘을 것이다.
왜냐면 행동이 상태를 불러오니까 !!
그리고 V(s)를 쓰든 Q(s,a)를 쓰든 같은 Policy를 내뱉을 것이다.
왜냐면 걍 접근방법의 차이지 환경은 같은 환경이니까 !!
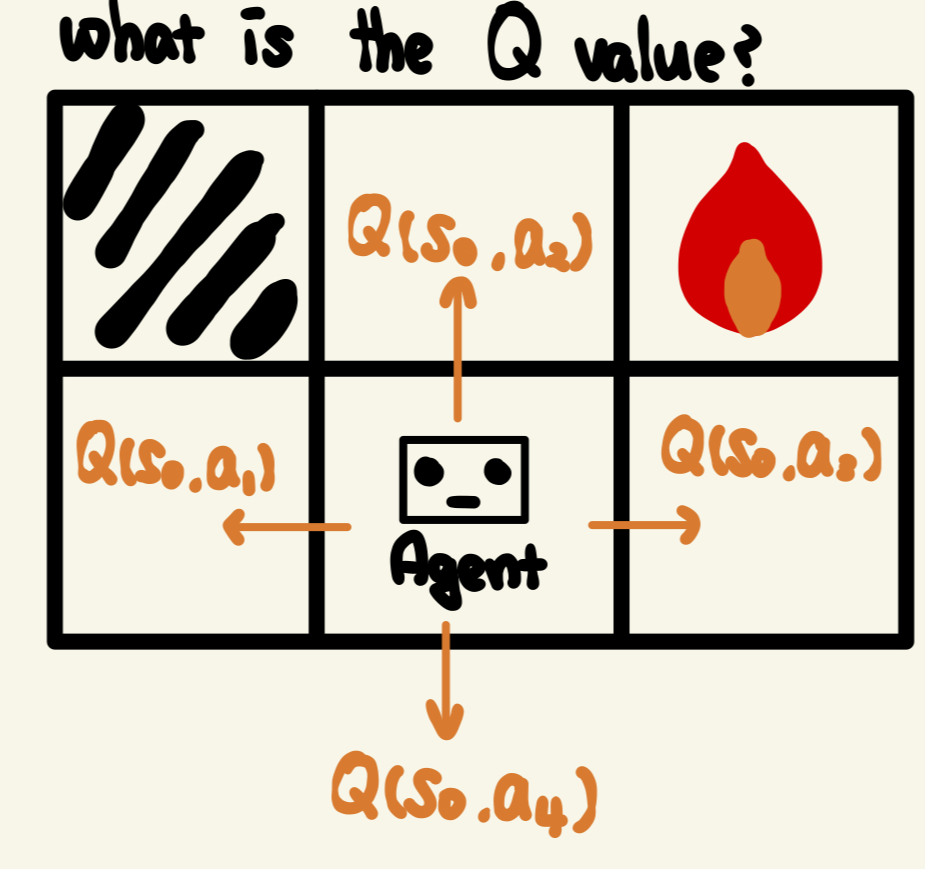
위로 올라가면 무슨 일이 생길까?
>> 우선, 위로 올라가는 상황에서, 가장 먼저 얻어 갈 수 있는 것은 $ R(s_0, a_2) $ 이다.
>> 따라서 우선은, $ Q(s_0,a_2) = R(s_0,a_2) + \dots $ 로 두자
위로 가려고 하면 또 무슨일이 생길까 ?
>> 에어전트가 새로운 상태 ($ s_2 $)에 놓이게 된다.
>> markov decision process이므로 위로 가려고 할때 80%의 확률로 위로 가겠지만,
10%의 확률로 오른쪽 혹은 왼쪽으로 갈 수도 있다.
어디로 실제 이동하든가 상관없이 새로운 상태에 대해 정량화된 측정 기준이 존재한다.
>> 그게 상태가치이다.
>> 그러나 다음과 같은경우, 가능한 상태가 3가지 ( $ s_1, s_2, s_3 $ ) 로 다양하므로
>> 새로운 상태의 "기댓값"을 넣어준다. (마찬가지로 할인계수도, 한걸음 이동하니까)
>> $ Q(s_0,a_2) = R(s_0,a_2) + \gamma \sum_{s^\prime} (P(s_0,a_2,s_\prime)V(s^\prime)) $
좀 더 일반적인 경우에 대해 정리를 해보면

다시한번 Q value modeling을 리마인드하자면
1. action을 통해 보상(R)을 받는다.
2. 새로운 상태로 가니까 상태가치를 추가해준다.
인데, 이렇게 모델링을 하다보니까 기존의 $ V(s) $ 식과 유사함을 알 수 있다.
그이유가 뭘까요?
생각해보면, 상태가치 $ V(s) $ 라는 것도 결과의 최댓값, 가능한 행동에 대한 최댓값으로 정의 했기 때문에 같을 수 밖에 없다.
즉, 상태가치란 가능한 모든 Q 값의 최댓값과 같다.
$$ V(s) = \underset{a} {max} [Q(s,a)] $$
사실 상태가치를 포스팅을 하면서 실제로 계산한적은 많이 없었는데,
이는 Markov Decision Process 개념이 추가된 이후 상태가치함수 $ V(s) $ 자체가
귀납적 함수라서 손으로는 쉽게 구할 수 없기 때문이다.
다시 본론으로 들어와서 우리는 아래 식을 조금 수정 할 생각이다.
$ V(s) = \underset{a} {max} [R(s,a) + \gamma \sum_{s^\prime} P(s,a,s^\prime)V(s^\prime)] $
$ Q(s,a) = R(s,a) + \gamma \sum_{s^\prime} P(s,a,s^\prime)V(s^\prime) $
에서
$ V(s) = \underset{a} {max} [Q(s,a)] $ 이므로
$ Q(s,a) = R(s,a) + \gamma \sum_{s^\prime} P(s,a,s^\prime)* \underset{a^\prime} {max} [Q(s^\prime,a^\prime)] $
로 수정할 수 있다.
이제 Q 값에 대한 귀납적 함수를 만들었다.
이제 이 식을 통해 Agent는 action의 퀄리티에 대해 이해할 것이다.
'Reinforcement learning 기초' 카테고리의 다른 글
| [Reinforcement Learning] Deep Q-learning Intuition (1) (0) | 2023.04.23 |
|---|---|
| [Reinforcement Learning] Temporal Difference (0) | 2023.04.18 |
| [Reinforcement Learning] Living Penalty (0) | 2023.04.15 |
| [Reinforcement Learning ] Policy vs Plan (0) | 2023.04.12 |
| [Reinforcement Learning] Markov Decision Process (0) | 2023.04.11 |




댓글